Statistika adalah
ilmu yang mempelajari bagaimana merencanakan, mengumpulkan,
menganalisis, menginterpretasi, dan mempresentasikan data. Singkatnya,
statistika adalah ilmu yang berkenaan dengan data. Istilah ‘statistika’
(bahasa Inggris: statistics) berbeda dengan ‘statistik’ (statistic). Statistika merupakan ilmu yang berkenaan dengan data, sedang statistik adalah data, informasi, atau hasil penerapan algoritma statistika pada suatu data.
Dari kumpulan data,
statistika dapat digunakan untuk menyimpulkan atau mendeskripsikan data;
ini dinamakan statistika deskriptif. Sebagian besar konsep dasar
statistika mengasumsikan teori probabilitas. Beberapa istilah statistika
antara lain: populasi, sampel, unit sampel, dan probabilitas.
DEFINISI PROBABILITAS
Harga angka yang
menunjukkan seberapa besar kemungkinan suatu peristiwa terjadi, di
antara keseluruhan peristiwa yang mungkin terjadi.
- Contoh 1:Sebuah mata uang logam mempunyai sisi dua (H & T) kalau mata uang tersebut dilambungkan satu kali, peluang untuk keluar sisi H adalah ½.
- Contoh 2:Sebuah dadu untuk keluar mata ‘lima’ saat pelemparan dadu tersebut satu kali adalah 1/6 (karena banyaknya permukaan dadu adalah 6)
Rumus :
P (E) = X/NP: ProbabilitasE: Event (Kejadian)X: Jumlah kejadian yang diinginkan (peristiwa)N: Keseluruhan kejadian yang mungkin terjadi
Di dalam suatu pabrik
ada 30 wanita dan 70 laki-laki. Sehabis makan siang yang disediakan
pabrik akan ditanyakan “apakah makanan tadi cukup baik”. Untuk itu akan
di undi (di acak) siapa orang yang akan ditanyakan pendapatnya.
Probabilitas akan terambil seorang buruh wanita adalah 30/100 -> P
(0,3)
Probabilitas yang rendah menunjukkan kecilnya kemungkianan suatu peristiwa akan terjadi.
Probabilitas adalah suatu perhitungan yang didasarkan pada peluang atau kemungkinan.Manfaat mempelajari probabilitas
sangat berguna untuk pengambilan keputusan yang tepat, karena kehidupan
di dunia tidak ada kepastian, sehingga diperlukan untuk mengetahui
berapa besar probabilitas suatu peristiwa akan terjadi. Probabilitas
dinyatakan dalam angka pecahan antara 0 sampai 1 atau dalam persentase.
Beberapa istilah penting dalam probabilitas adalah:
- Percobaan
- Hasil
- Peristiwa
- Pendekatan klasik yang memberikan probabilitas yang sama.
- Pendekatan frekuensi relatif yang memperhatikan kejadian yang telah terjadi.
- Pendekatan subjektif berdasarkan penilaian individu.
Probabilitas/peluang merupakan banyaknya kemungkinan-kemungkinan pada suatu kejadian berdasarkan frekuensinya.
Jika ada a kemungkinan
yang dapat terjadi pada kejadian A dan ada b kemungkinan yang dapat
terjadi pada kejadian A, serta masing-masing kejadian mempunyai
kesempatan yang sama dan saling asing, maka probabilitas/peluang bahwa
akan terjadi a adalah:
P (A) = a/a+b ; dan peluang bahwa akan terjadi b adalah: P (A) = b/a+b
Contoh:
Pelamar pekerjaan
terdiri dari 10 orang pria (A) dan 15 orang wanita (B). Jika yang
diterima hanya 1, berapa peluang bahwa ia merupakan wanita?
Jawab:
P (A) = 15/10+15 = 3/5
2. PENDEKATAN FREKUENSI RELATIF
Nilai
probabilitas/peluang ditentukan atas dasar proporsi dari kemungkinan
yang dapat terjadi dalam suatu observasi/percobaan (pengumpulan data).
Jika pada data sebanyak
N terdapat a kejadian yang bersifat A, maka probabilitas/peluang akan
terjadi A untuk N data adalah: P (A) = a/N
Contoh:
Dari hasil penelitian
diketahui bahwa 5 orang karyawan akan terserang flu pada musim dingin.
Apabila lokakarya diadakan di Puncak, berapa probabilitas terjadi 1
orang sakit flu dari 400 orang karyawan yang ikut serta?
Jawab:
P (A) = 5/400 = P (A) = 1/80
3. PENDEKATAN SUBYEKTIF
Nilai
probabilitas/peluang adalah tepat/cocok apabila hanya ada satu
kemungkinan kejadian terjadi dalam suatu kejadian ditentukan berdasarkan
tingkat kepercayaan yang bersifat individual (misalnya berdasarkan
pengalaman).
Probabilitas disajikan dengan symbol P,
sehingga P(A) menyatakan probabilitas bahwa kejadian A akan terjadi
dalam observasi atau percobaan tunggal, dengan 0 ≤ P(A) ≤ 1.
Dalam suatu observasi/percobaan
kemungkinan kejadian ada 2, yaitu “terjadi (P(A)) atau “tidak terjadi”
(P(A)’), maka jumlah probabilitas totalnya adalah P(A) + P(A)’ = 1
Dalam perhitungan probabilitas ada beberapa asas peristiwa yang sering terjadi, yaitu:- Asas peristiwa mutually exclusive.
- Asas peristiwa non exclusive (tidak saling asing).
- Asas peristiwa independen (bebas) yang mencakup tiga bagian: marginal, gabungan, dan peluang bersyarat.
- Dependen , yang terbagi dalam tiga bagian: marginal, gabungan, dan peluang bersyarat.
Distribusi probabilitas (peluang) adalah sebuah daftar dari keseluruhan hasil suatu percobaan kejadian yang disertai dengan nilai probabilitas masing-masing hasil (event).
Perhitungan Nilai Peluang Hukum Probabilitas
Asas perhitungan probabilitas dengan berbagai kondisi yang harus diperhatikan:
1. Hukum Pertambahan
terdapat 2 kondisi yang harus diperhatikan yaitu:
- Mutually Exclusive (saling meniadakan)
Rumus: P (A U B) = P (A atau B)= P (A) + P (B)
Contoh:
Probabilitas untuk keluar mata 2 atau mata 5 pada pelemparan satu kali sebuah dadu adalah:
P(2 U 5) = P (2) + P (5) = 1/6 + 1/6 = 2/6
- Non Mutually Exclusive (dapat terjadi bersama)
Peristiwa Non Mutually Exclusive (Joint) dua peristiwa atau lebih dapat terjadi bersama-sama (tetapi tidak selalu bersama. Contoh penarikan kartu as dan berlian
P (A U B) =P(A) + P (B) – P(A ∩B)
Peristiwa terjadinya A
dan B merupakan gabungan antara peristiwa A dan peristiwa B. Akan tetapi
karena ada elemen yang sama dalam peristiwa A dan B, gabungan peristiwa
A dan B perlu dikurangi peristiwa di mana A dan B memiliki elemen yang
sama.
Dengan demikian,
probabilitas pada keadaan di mana terdapat elemen yang sama antara
peristiwa A dan B maka probabilitas A atau B adalah probabilitas A
ditambah probabilitas B dan dikurangi probabilitas elemen yang sama
dalam peristiwa A dan B.
2. HUKUM PERKALIAN
Terdapat dua kondisi yang harus diperhatikan apakah kedua peristiwa tersebut saling bebas atau bersyarat.
- Peristiwa Bebas (Independent)
Apakah kejadian atau
ketidakjadian suatu peristiwa tidak mempengaruhi peristiwa lain. Contoh:
Sebuah coin dilambungkan 2 kali maka peluang keluarnya H pada lemparan
pertama dan pada lemparan kedua saling bebas.
P(A ∩B) = P (A dan B) = P(A) x P(B)
Contoh soal 1:
Sebuah dadu dilambungkan dua kali, peluang keluarnya mata 5 untuk kedua kalinya adalah:
P (5 ∩ 5) = 1/6 x 1/6 = 1/36
Contoh soal 2:
Sebuah dadu dan koin dilambungkan
bersama-sama, peluang keluarnya hasil lambungan berupa sisi H pada koin
dan sisi 3 pada dadu adalah:
P (H) = ½, P (3) = 1/6
P (H ∩ 3) = ½ x 1/6 = 1/12
- Peristiwa tidak bebas (Hk. Perkalian)
Peristiwa tidak bebas > peristiwa bersyarat (Conditional Probability).
Dua peristiwa dikatakan
bersyarat apabila kejadian atau ketidakjadian suatu peristiwa akan
berpengaruh terhadap peristiwa lainnya.
Contoh:
Dua buah kartu ditarik dari set kartu bridge dan tarikan kedua tanpa
memasukkan kembali kartu pertama, maka probabilitas kartu kedua sudah
tergantung pada kartu pertama yang ditarik.
Simbol untuk peristiwa bersyarat adalah P (B│A) -> probabilitas B pada kondisi A
P(A ∩B) = P (A) x P (B│A)
Contoh :
Dua kartu ditarik dari satu set kartu
bridge, peluang untuk yang tertarik keduanya kartu as adalah sebagai
berikut: Peluang as I adalah 4/52 -> P (as I) = 4/52
Peluang as II dengan syarat as I sudah tertarik adalah 3/51
P (as II │as I) = 3/51
P (as I ∩ as II) = P (as I) x P (as II│ as I) = 4/52 x 3/51 = 12/2652 =1/221
Prinsip Menghitung - Faktorial Bilangan Asli
Definisi : Hasil
perkalian semua bilangan bulat positif secara berurutan dari 1 sampai
dengan n disebut n faktorial. Dari definisi faktorial tersebut, maka
dapat dituliskan prinsip menghitung faktorial sebagai berikut :
n ! = n x (n-1) x (n-2) x (n-3) x … 3 x 2 x 1
n ! dibaca n faktorial
Telah diambil kesepakatan bahwa : 0 ! = 1
Contoh:
6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
- Kombinasi
Kombinasi adalah campuran atau gabungan
atau susunan dari semua atau sebagian elemen dari suatu himpunan yang
tidak mementingkan urutan elemen.
Kombinasi dapat dirumuskan sebagai berikut :
n = n! /r ! ( n – r )!
Contoh :
Untuk
pemilihan 4 mahasiswa menjadi pengurus himpunan mahasiswa jurusan
matematika FMIPA UNM terdapat 8 mahasiswa prodi pendidikan matematika
dan 6 mahasiswa prodi matematika yang memenuhi syarat untuk dipilih.
Berapa banyak cara memilih pengurus bila semua anggota pengurus dari
prodi yang sama?
Jawaban :
Dari prodi pendidikan matematika 8 orang, harus dipilih 4 orang. Berarti kita hitung dengan menggunakan C (8,4) = 70 cara
Sedangkan dari prodi matematika, kita dapat memilih dengan C (6,4) = 6!/2!4! = 36x5x4!/2×4! = 15 cara.
Sehingga
jika yang terpilih adalah mahasiswa dari prodi yang sama, kemungkinan
banyak cara memilih adalah C (8,4) + C (6,4) = 70 + 15 = 85 cara.
- Permutasi
Permutasi adalah
menggabungkan beberapa objek dari suatu grup dengan memperhatikan
urutan. Di dalam permutasi, urutan diperhatikan.
{1,2,3} tidak sama dengan {2,3,1} dan {3,1,2}
Contoh:
Ada sebuah kotak berisi
3 bola masing-masing berwarna merah, hijau dan biru. Jika seorang anak
ditugaskan untuk mengambil 2 bola secara acak dan urutan pengambilan
diperhatikan, ada berapa permutasi yang terjadi?
Jawaban:
Ada 6 permutasi yaitu; M-H, M-B, H-M, H-B, B-M, B-H.
Permutasi Tanpa Pengulangan
Jika urutan diperhatikan dan setiap objek
yang tersedia hanya bisa dipilih atau dipakai sekali maka jumlah
permutasi yang ada adalah:
di mana n adalah jumlah objek yang dapat kamu pilih, r adalah jumlah yang harus dipilih dan ! adalah simbol faktorial.
Contoh:
ada sebuah pemungutan
suara dalam suatu organisasi. Kandidat yang bisa dipilih ada lima orang.
Yang mendapat suara terbanyak akan diangkat menjadi ketua organisasi
tersebut. Yang mendapat suara kedua terbanyak akan diangkat menjadi
wakil ketua. Dan yang mendapat suara ketiga terbanyak akan menjadi
sekretaris. Ada berapa banyak hasil pemungutan suara yang mungkin
terjadi? Dengan menggunakan rumus di atas maka ada 5!/(5-3)! = 60
permutasi.
Umpamakan jika n = r (yang menandakan bahwa jumlah objek yang bisa dipilih sama dengan jumlah yang harus dipilih) maka rumusnya menjadi:
Contoh:
ada lima kotak kosong
yang tersedia. Kelima kotak kosong itu harus diisi (tidak boleh ada yang
kosong). Kelima kotak kosong itu hanya boleh diisi dengan angka
1,2,3,4,5. Ada berapa banyak cara untuk mengisi kotak kosong? Dengan
menggunakan rumus n! maka ada 5! = 120 permutasi.
Permutasi Pengulangan (dari unsur-unsur yang sama)
Dari huruf-huruf pada kata MATEMATIKA,
berapa banyaknya pasangan huruf yang dapat dibentuk? Jika mengingat
kembali tentang permutasi, seharusnya banyaknya pasangan yang dapat
dibentuk adalah sebanyak 10! pasangan.
Namun, apakah M1A1TEM2A2TIKA3 sama dengan M1A3TEM2A2TIKA1?
Ambil P sebagai jumlah permutasi berbeda
untuk kesepuluh huruf. Jumlah permutasi dari kedua huruf M adalah 2!
dan jumlah permutasi dari ketiga huruf A adalah 3! Sehingga jumlah
total permutasi adalah 2! x 3! x P.
Dengan demikian, diperoleh : 2!3!P = 10! Sehingga :
Contoh tersebut mengantarkan kita kepada
definisi permutasi yang mengandung unsur yang sama: Misalnya suatu
himpunan yang terdiri atas n elemen memiliki r1 elemen jenis pertama
yang sama, r2 elemen jenis kedua yang sama, ., dan rk elemen jenis ke k
yang sama, dengan :
r1 + r2 + . rk < n
maka banyak permutasi berbeda dari n elemen diberikan oleh :
Contoh :
- Jika huruf-huruf pada kata “BOROBUDUR” dipertukarkan, berapa banyak susunan huruf berbeda yang dapat diperoleh?
Jawaban :
Pada kata BOROBUDUR
terdapat 9 huruf dengan huruf B diulang 2 kali, huruf O diulang 2 kali,
huruf R diulang 2 kali, dan huruf U diulang 2 kali. Banyaknya susunan
huruf berbeda yang diperoleh diberikan oleh rumus berikut:
Permutasi Siklis
Permutasi siklis menganggap elemen disusun secara melingkar.
h a
g b
f c
e d
Dengan menganggap panjang untai (atau banyaknya elemen) adalah n, dan karena elemen awal tidak boleh diubah-ubah posisinya, maka banyaknya elemen yang dapat berubah-ubah posisinya adalah n-1. Dengan demikian kita cukup mempermutasikan elemen yang dapat berubah-ubah posisi saja, yaitu sebanyak  .
.
 .
.
Contoh :
Sebuah
keluarga terdiri atas 5 orang. Mereka akan duduk mengelilingi sebuah
meja bundar untuk makan bersama. Berapa banyaknya cara agar mereka dapat
duduk mengelilingi meja makan tersebut dengan urutan yang berbeda?
Jawaban :
Banyaknya cara agar 5 orang dapat duduk mengelilingi meja makan sama dengan banyak permutasi siklis 5 elemen, yaitu :
(5 -1)! = 4! = 4 x 3 x 2 x 1 = 24
Dengan menganggap panjang untai (atau banyaknya elemen) adalah n, dan karena elemen awal tidak boleh diubah-ubah posisinya, maka banyaknya elemen yang dapat berubah-ubah posisinya adalah n-1. Dengan demikian kita cukup mempermutasikan elemen yang dapat berubah-ubah posisi saja, yaitu sebanyak 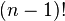 .
.
Teorema Bayes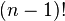 .
.
Dalam teori probabilitas dan statistika, teorema Bayes adalah sebuah teorema dengan dua penafsiran berbeda. Dalam penafsiran Bayes, teorema ini menyatakan seberapa jauh derajat kepercayaan subjektif harus berubah secara rasional ketika ada petunjuk baru.
Dalam penafsiran frekuentis
teorema ini menjelaskan representasi invers probabilitas dua kejadian.
Teorema ini merupakan dasar dari statistika Bayes dan memiliki penerapan
dalam sains, rekayasa, ilmu ekonomi (terutama ilmu ekonomi mikro),
teori permainan, kedokteran dan hukum. Penerapan teorema Bayes untuk
memperbarui kepercayaan dinamakan inferens Bayes.
Rumus Teori Bayes :
 Jadi, bisa dinyatakan P(A|B) berarti peluang kejadian A bila B terjadi dan P(B|A) berarti peluang kejadian B bila A terjadi.
Jadi, bisa dinyatakan P(A|B) berarti peluang kejadian A bila B terjadi dan P(B|A) berarti peluang kejadian B bila A terjadi.
Diagram Pohon merupakan
suatu diagram yang menyerupai pohon dimulai dari batang kemudian menuju
ranting dan daun. diagram pohon dimaksudkan untuk membantu
menggambarkan probabilitas atau probabilitas bersyarat dan probabilitas
bersama. diagram pohon sangat berguna untuk menganaliusis
keputusan-keputusan dimana terdapat tahapan-tahapan pekerjaan.






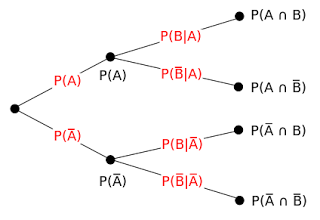
Lengkapin lagi ya.
BalasHapusKunjungi juga http://mathcyber1997.com